04. Teoria mnogości - część 1
Contents
04. Teoria mnogości - część 1#
Tresci kształcenia: Podstawy teorii mnogości. Zbiory i operacje na zbiorach. Pojęcie zbioru, zbioru pustego, elementu, należenia, inkluzji. Podzbiory prostej rzeczywistej, przedziały, suma, przekrój, różnica zbiorów. Zbiory przeliczalne i nieprzeliczalne.
Efekty kształcenia: Student potrafi wykonać podstawowe operacje na zbiorach, określić ich przeliczalność.
Wstęp#
Podczas tych zajęć zajmiemy się pojęciem zbioru, kluczowym dla całej matematyki. Intuicyjnie, zbiorem nazywamy pewną kolekcję obiektów. Przyjmujemy, że pojęcie zbioru oraz pojęcie należenia do zbioru są pojęciami pierwotnymi, tzn. nie wymagają one definicji.
Zapis \(a \in A\) oznacza, że obiekt \(a\) jest elementem zbioru \(A\). Przykładowo, \(2 \in \mathbb N\) (tzn. dwa należy do zbioru liczb naturalnych). Aby powiedzieć, że a nie jest elementem zbioru \(A\), zapisujemy \(a \not \in A\).
Najprostszym sposobem określenia zbioru jest wyliczenie jego elementów. Przykładowo \(\{ 1, 2, 3 \}\) to zbiór złożony z trzech elementów - 1, 2 oraz 3. Wyliczenia możemy też dokonać, w sposób skrócony, za pomocą trzykropka, jeżeli jasne jest jakie elementy mamy na myśli. Przykładowo:
\(\{ 1, 2, \ldots, 2000 \}\) oznacza zbiór, którego elementami są liczby od 1 do 2020,
\(\{ 2, 4, 6, 8, 10, \ldots \}\) oznacza zbiór dodatnich liczb parzystych.
Innym sposobem zdefiniowania zbioru jest określenie warunku, który mają spełniać jego elementy. Zbiór taki zapisujemy w następujący sposób:
Przykładowo
oznacza zbiór liczb rzeczywistych \(x\), które spełniają równanie \((x-1) \cdot (x-2) = 0\). Zbiór ten można zapisać również w taki sposób:
a także w taki: \(\{1, 2\}\).
Przykłady zbiorów#
Szczególny przykład zbioru stanowi zbiór pusty, oznaczany jako \(\varnothing\). Jest to zbiór, który nie ma żadnych elementów. Literami \(\mathbb R\), \(\mathbb Q\), \(\mathbb Z\), \(\mathbb N\) oznacza się zazwyczaj zbiory liczb rzeczywistych, wymiernych, całkowitych i naturalnych.
Przedziały liczbowe to podzbiory zbioru liczb rzeczywistych, czyli liczby które znajdują się między dwiema danymi. Istnieją cztery rodzaje przedziałów:
przedziały otwarte: \((a, b) = \{ x \in \mathbb R : a < x < b \}\)
przedziały domknięte: \([a, b] = \{ x \in \mathbb R : a \le x \le b \}\)
przedziały lewostronnie domknięte: \([a, b) = \{ x \in \mathbb R : a \le x < b \}\)
przedziały prawostronnie domknięte: \((a, b] = \{ x \in \mathbb R : a < x \le b \}\)
Różnią się one tym, czy końce przedziałów (liczby \(a\) i \(b\)) należą do nich. Dodatkowo rozpatruje się przedziały nieograniczone, w których lewy koniec oznacza się jako \(-\infty\) lub też prawy przez \(\infty\). Przykładowo:
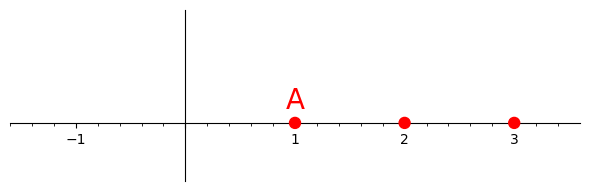
Rysując przedziały na osi liczb rzeczywistych, oznaczamy ich końce kółkami (zamalowanym kółkiem, jeżeli koniec należy do przedziału, i pustym w przeciwnym wypadku).
#Struktura RealSet w Sage'u pozwala na operowanie przedziałami osi rzeczywistej oraz ich sumami.
A = RealSet(1, 3)
B = RealSet([1, 3])
C = RealSet.closed_open(1, 3)
D = RealSet.open_closed(1, 3)
print("A = ", A)
print("B = ", B)
print("C = ", C)
print("D = ", D)
A = (1, 3)
B = [1, 3]
C = [1, 3)
D = (1, 3]
##Narysujemy teraz podane zbiory. Niestety, nie istnieje gotowa funkcja Sage'a pozwalająca na to.
A = RealSet(1, 3)
B = RealSet([1, 3])
C = RealSet.closed_open(1, 3)
D = RealSet.open_closed(1, 3)
## Ten kod służy do rysowania podzbiorów prostej rzeczywistej w zadanym kolorze i z zadanym podpisem.
def narysuj_przedzial(realset, kolor='blue', tekst=""):
i = 0
wynik = text("", (0, 0))
try:
while (i>=0):
odcinek = realset.get_interval(i)
a, b = odcinek.lower(), odcinek.upper()
if a == b and odcinek.lower_closed() and odcinek.upper_closed():
wynik += circle((a, 0), 0.05, fill=True, rgbcolor = kolor)
i += 1
else:
if a == -oo:
a = -4
lewy_koniec = text("", (0, 0))
else:
lewy_koniec = circle((a, 0), 0.05, rgbcolor = kolor, fill = odcinek.lower_closed())
if b == oo:
b = 4
prawy_koniec = text("", (0, 0))
else:
prawy_koniec = circle((b, 0), 0.05, rgbcolor = kolor, fill = odcinek.upper_closed())
wynik += polygon2d([(a,0), (a+0.1,0.1), (b-0.1,0.1), (b,0)], alpha=0.5, rgbcolor = kolor)+lewy_koniec+prawy_koniec
if i==0:
wynik += text(tekst, ((a+b)/2,0.2), color = kolor, fontsize = 20)
i+=1
except:
return wynik
## Narysujmy podane zbiory
narysuj_przedzial(A, tekst = "Przedział (1, 3)").show(ticks = [None, []])
narysuj_przedzial(B, tekst = "Przedział [1, 3]").show(ticks = [None, []])
narysuj_przedzial(C, tekst = "Przedział [1, 3)").show(ticks = [None, []])
narysuj_przedzial(D, tekst = "Przedział (1, 3]").show(ticks = [None, []])




Równość zbiorów#
Jak stwierdzić, czy dwa zbiory są równe? Służy do tego następująca zasada.
Zasada ekstensjonalności
Zbiory \(A\) i \(B\) są równe wtedy, i tylko wtedy gdy mają takie same elementy.
Intuicyjnie mówiąc oznacza to, że przy określaniu zbioru nie ma znaczenia kolejność elementów, ani to ile razy zostały one wypisane. Przykładowo zbiory \(A = \{ 1, 2, 1 \}\) oraz \(B = \{ 2, 1 \}\) są równe, ponieważ elementami każdego z tych zbiorów są dwie liczby - 1 oraz 2. Nie ma znaczenia kolejność, w jakiej je wypisaliśmy oraz fakt, że jedna z nich była wypisana dwukrotnie.
# Python posiada zaimplementowaną strukturę zbioru. Jest to struktura, w której nie jest ważna kolejność
# ani liczba wystąpień elementu.
A = Set([1, 2, 1])
B = Set([2, 1])
print(A==B)
True
Przykład#
Podaj, ile różnych elementów mają zbiory \(A = \{x \in \mathbb Z : x^2 < 9 \}\) oraz \(B = \{ 1, \{1\}, \{1, \{1\} \}\} \) i wymień je.
Rozwiązanie#
Nierówność \(x^2 < 9\) jest spełniona wtedy i tylko wtedy, gdy \(|x| < 3\). Zatem zbiór \(A\) ma 5 elementów: -2, -1, 0, 1, 2.
Zbiór \(B = \{ \color{red} 1 , \color{green} { \{1\} }, \color{blue} {\{1, \{1\} \} } \}\) ma 3 elementy:
liczbę \({\color{red}1}\),
\(\color{green}{\{ 1 \} }\) (zbiór jednoelementowy złożony z liczby 1),
\(\color{blue}{\{ 1, \{1 \} \} }\) (zbiór dwuelementowy złożony z liczby 1 oraz ze zbioru jednoelementowego \(\{ 1 \}\)).
Zauważmy, że te elementy są między sobą różne. Przykładowo, \(\color{red}{1} \neq \color{green}{\{ 1 \} }\), ponieważ \(\color{red}{ 1 }\) jest liczbą, a \(\color{green}{\{ 1 \}}\) - zbiorem.
B = Set([1, Set([1]), Set([1, Set([1])])]) #to jest zbiór B z zadania
#Ile elementów ma zbiór B?
print(B.cardinality())
3
Podzbiory#
Omówimy teraz pojęcie podzbioru.
Definicja
Mówimy, że zbiór \(A\) jest podzbiorem zbioru \(B\), jeżeli każdy element zbioru \(A\) jest też elementem zbioru \(B\). Zapisujemy to w następujący sposób: \(A \subset B\).
Jako prosty przykład zauważmy, że \(\mathbb N \subset \mathbb R\), ponieważ każda liczba naturalna jest rzeczywista.
Przykład#
Rozważmy zbiory \(A = \{ 1 \}\) oraz \(B = \{\{1\}, 1, \varnothing \}\). Czy zachodzi \(A \subset B\) lub też \(B \subset A\)?
Jedyny element \(A\), czyli liczba jeden, należy do zbioru \(B\). Zatem \(A \subset B\).
Z drugiej strony \(B\) nie jest podzbiorem \(A\). Istotnie, zbiór \(\{ 1 \}\) jest elementem B, ale \(\{ 1 \} \not \in A\) (jedynym elementem zbioru \(A\) jest liczba 1, a nie zbiór jednoelementowy \(\{ 1 \}\)!).
#Sprawdzimy, czy A jest podzbiorem B, i czy B jest podzbiorem A.
A = Set([1])
B = Set([Set([1]), 1, Set([])])
print(A.issubset(B))
print(B.issubset(A))
True
False
Przykład#
Ile podzbiorów ma zbiór \(A = \{ 1, \{1 \} , \{ \{1 \} \} \}\)?
Zbiór \(A = \{ { \color{red} 1 }, \color{green} { \{1 \} }, \color{blue} { \{ \{1 \} \} } \}\) ma osiem podzbiorów:
jeden podzbiór zeroelementowy, tzn. zbiór pusty \(\varnothing\),
trzy podzbiory jednoelementowe: \(\{ \color{red} { 1 } \}\), \(\{ \color{green} { \{ 1 \} } \}\), \(\{ \color{blue}{\{ \{ 1 \} \} } \}\),
trzy podzbiory dwuelementowe: \(\{ \color{red}{ 1}, \color{green}{ \{1 \} } \}\), \(\{ \color{red}{ 1}, \color{blue}{ \{ \{1 \} \} } \}\), \(\{ \color{green} { \{1 \} }, \color{blue}{ \{ \{1 \} \} } \}\)
jeden podzbiór trzyelementowy (cały zbiór): \(\{ \color{red}{ 1}, \color{green}{ \{1 \} }, \color{blue}{\{ \{1 \} \} } \}\)
#Wypiszmy podziory A.
A = Set([1, Set([1]), Set([Set([1])])])
for C in A.subsets():
print(C)
{}
{1}
{{1}}
{{{1}}}
{1, {1}}
{1, {{1}}}
{{1}, {{1}}}
{1, {1}, {{1}}}
Operacje na zbiorach#
Przedstawimy teraz cztery podstawowe operacje na zbiorach. Przypomnijmy krótko, że symbol \(\wedge\) oznacza “i”, zaś symbol \(\vee\) oznacza “lub”.
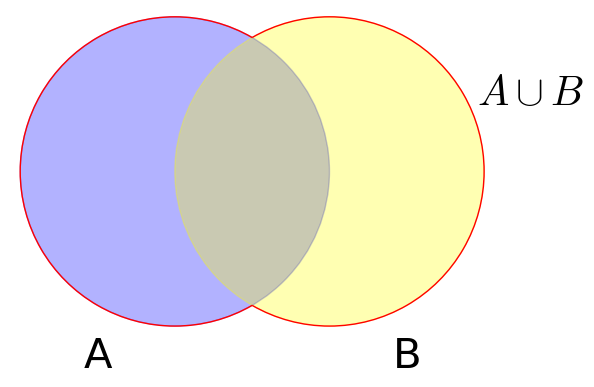
Sumą zbiorów \(A\) i \(B\) nazwiemy zbiór:
tzn. zbiór złożony z tych elementów, które należą do zbioru A lub do zbioru B.
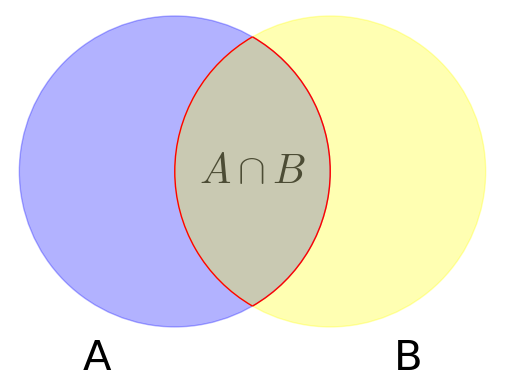
Przekrojem zbiorów \(A\) i \(B\) nazwiemy zbiór:
tzn. zbiór złożony z tych elementów, które należą do zbioru A oraz do zbioru B. Jeżeli \(A \cap B = \varnothing\) (tzn. A i B) nie mają wspólnych elementów, to mówimy, że A i B są rozłączne.
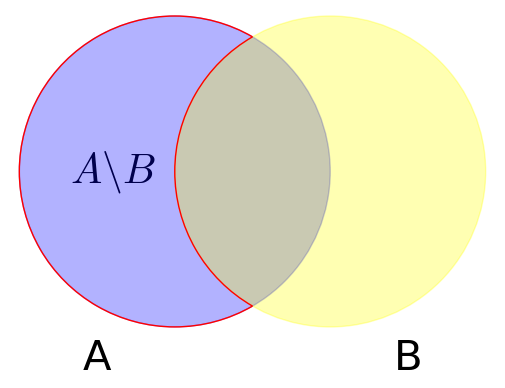
Różnicą zbiorów \(A\) i \(B\) nazwiemy zbiór:
tzn. zbiór złożony z tych elementów, które należą do zbioru A, ale nie należą do zbioru B.
Jeżeli zbiór \(A\) jest częścią pewnego ustalonego zbioru \(X\), definiujemy również dopełnienie zbioru \(A\), jako elementy, które nie należą do \(A\):
Przykładowo dopełnieniem zbioru liczb wymiernych (w zbiorze liczb rzeczywistych) jest zbiór liczb niewymiernych.
Mówiąc o operacjach na zbiorach używamy często tzw. diagramów Venna. Do zobrazowania zbiorów i operacji na nich wykorzystuje się wówczas figury płaskie, zazwyczaj okręgi. Argument za pomocą diagramów Venna nie stanowi dowodu, ale pomaga w intuicyjnym zrozumieniu działań na zbiorach.
#kod pomocniczy generujący diagramy Venna
A = circle((0, 0), 1, color = 'blue', fill=True, alpha=0.3) + text('A',(-0.5,-1.2),rgbcolor='black', fontsize=30)
B = circle((1, 0), 1, color = 'yellow', fill=True, alpha=0.3) + text('B',(1.5,-1.2),rgbcolor='black', fontsize=30)
AsumB = arc((0,0), 1, sector=(pi/3, 5*pi/3), color='red')+arc((1,0), 1, sector=(pi+pi/3, pi+5*pi/3), color='red')+text(r'$A \cup B$',(2.3,0.5),rgbcolor='black', fontsize=30)
(A+B+AsumB).show(axes=false)
AcapB = arc((0,0), 1, sector=(-pi/3,pi/3), color='red')+arc((1,0), 1, sector=(2*pi/3,4*pi/3), color='red')+text(r'$A \cap B$',(0.5,0),rgbcolor='black', fontsize=30)
(A+B+AcapB).show(axes=false)
AminB = arc((0,0), 1, sector=(pi/3, 5*pi/3), color='red')+arc((1,0), 1, sector=(2*pi/3,4*pi/3), color='red')+text(r'$A \backslash B$',(-0.4,0),rgbcolor='black', fontsize=30)
(A+B+AminB).show(axes=false)
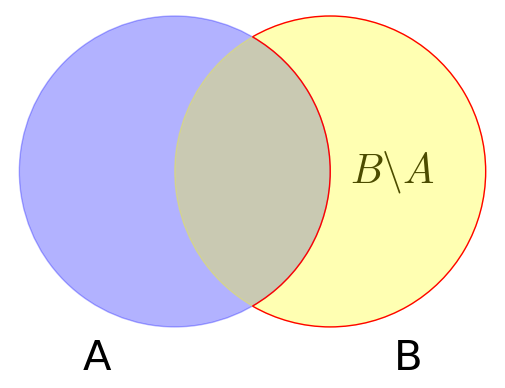
BminA = arc((1,0), 1, sector=(pi+pi/3, pi+5*pi/3), color='red')+arc((0,0), 1, sector=(pi+2*pi/3,pi+4*pi/3), color='red')+text(r'$B \backslash A$',(1.4,0),rgbcolor='black', fontsize=30)
(A+B+BminA).show(axes=false)
Przykład#
Znajdź \(A \cup B\), \(A \cap B\), \(A \setminus B\) oraz \(B \setminus A\) dla następujących zbiorów:
(a) \(A = (−\infty; 3)\), \(B = [-1; 4)\),
(b) \(A = \{ 1, 2, 3 \}\), \(B = [-1, 2) \cup \{ 3 \}\).
W każdym z przypadków narysuj wynik.
Rozwiązanie#
#(a)
A1 = RealSet(-oo, 3)
B1 = RealSet.closed_open(-1, 4)
#suma A oraz B
A1_suma_B1 = A1.union(B1)
pretty_print(LatexExpr("A \\cup B=" + str(A1_suma_B1)))
#przekrój A i B
A1_przekroj_B1 = A1.intersection(B1)
pretty_print(LatexExpr("A \\cap B=" + str(A1_przekroj_B1)))
#różnica A i B
A1_roznica_B1 = A1.difference(B1)
pretty_print(LatexExpr("A \\setminus B=" + str(A1_roznica_B1)))
#różnica B i A
B1_roznica_A1 = B1.difference(A1)
pretty_print(LatexExpr("B \\setminus A=" + str(B1_roznica_A1)))
#(b)
A2 = RealSet([1, 1], [2, 2], [3, 3])
#Aby zdefiniować B, potrzebujemy dwóch zbiorów pomocnicznych:
P1 = RealSet.closed_open(-1, 2) #zbiór pomocniczy
P2 = RealSet([3, 3]) #zbiór pomocniczy
B2 = P1.union(P2) #B jest sumą dwóch zbiorów pomocniczych
#suma A oraz B
A2_suma_B2 = A2.union(B2)
pretty_print(LatexExpr("A \\cup B=" + str(A2_suma_B2)))
#przekrój A i B
A2_przekroj_B2 = A2.intersection(B2)
pretty_print(LatexExpr("A \\cap B=" + str(A2_przekroj_B2)))
#różnica A i B
A2_roznica_B2 = A2.difference(B2)
pretty_print(LatexExpr("A \\setminus B=" + str(A2_roznica_B2)))
#różnica B i A
B2_roznica_A2 = B2.difference(A2)
pretty_print(LatexExpr("B \\setminus A=" + str(B2_roznica_A2)))
## Ten kod służy do rysowania podzbiorów prostej rzeczywistej w zadanym kolorze i z zadanym podpisem.
def narysuj_przedzial(realset, kolor='blue', tekst=""):
i = 0
wynik = text("", (0, 0))
try:
while (i>=0):
odcinek = realset.get_interval(i)
a, b = odcinek.lower(), odcinek.upper()
if a == b and odcinek.lower_closed() and odcinek.upper_closed():
wynik += circle((a, 0), 0.05, fill=True, rgbcolor = kolor)
if i==0:
wynik += text(tekst, (a,0.2), color = kolor, fontsize = 20)
i += 1
else:
if a == -oo:
a = -4
lewy_koniec = text("", (0, 0))
else:
lewy_koniec = circle((a, 0), 0.05, rgbcolor = kolor, fill = odcinek.lower_closed())
if b == oo:
b = 4
prawy_koniec = text("", (0, 0))
else:
prawy_koniec = circle((b, 0), 0.05, rgbcolor = kolor, fill = odcinek.upper_closed())
wynik += polygon2d([(a,0), (a+0.1,0.1), (b-0.1,0.1), (b,0)], alpha=0.5, rgbcolor = kolor)+lewy_koniec+prawy_koniec
if i==0:
wynik += text(tekst, ((a+b)/2,0.2), color = kolor, fontsize = 20)
i+=1
except:
return wynik
#(a)
(narysuj_przedzial(A1.union(B1), tekst = r"$A \cup B$", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(A1.intersection(B1), tekst = r"$A \cap B$", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(A1.difference(B1), tekst = r'$A \backslash B$', kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(B1.difference(A1), tekst = r"$B \backslash A$", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, aspect_ratio = 1, ticks=[None, []])




#(b)
(narysuj_przedzial(A2, tekst = "A", kolor = 'red')).show(ymin = -0.5, ymax = 1, xmin = -1.5, xmax = 3.5, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(B2, tekst = "B", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, xmin = -1.5, xmax = 3.5, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(A2.union(B2), tekst = r"$A \cup B$", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, xmin = -1.5, xmax = 3.5, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(A2.intersection(B2), tekst = r"$A \cap B$", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, xmin = -1.5, xmax = 3.5, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(A2.difference(B2), tekst = r'$A \backslash B$', kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, xmin = -1.5, xmax = 3.5, aspect_ratio = 1, ticks=[None, []])
(narysuj_przedzial(B2.difference(A2), tekst = r"$B \backslash A$", kolor = 'blue')).show(ymin = -0.2, ymax = 0.4, xmin = -1.5, xmax = 3.5, aspect_ratio = 1, ticks=[None, []])





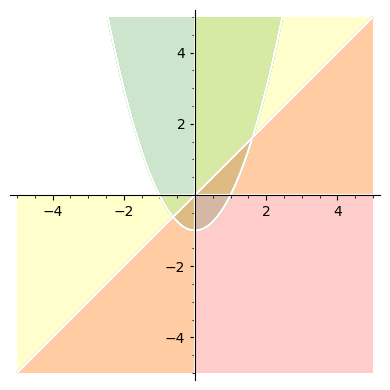
Przykład#
Rozważmy następujące podzbiory płaszczyzny rzeczywistej:
Narysuj zbiory \(A \cap B \cap C\) oraz \((A \cup B) \setminus C\).
var('x', 'y')
A = region_plot([y >= x^2 - 1],(x,-5,5),(y,-5,5), alpha = 0.2, incol = 'green')
B = region_plot([x*y > 0],(x,-5,5),(y,-5,5), alpha = 0.2, incol = 'yellow')
C = region_plot([x >= y], (x,-5,5), (y,-5,5), alpha = 0.2, incol = 'red')
#Narysujmy wszystkie trzy obszary.
(A + B + C).show()
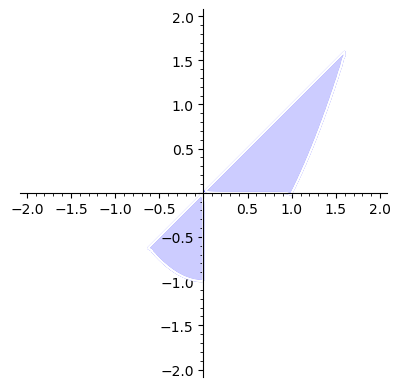
#Przekrój tych zbiorów to zbió określony przez wszystkie podane warunki
A_przekroj_B_przekroj_C = region_plot([y >= x^2 - 1, x >= y, x*y > 0],(x,-2,2),(y,-2,2), alpha = 0.2)
A_przekroj_B_przekroj_C.show()
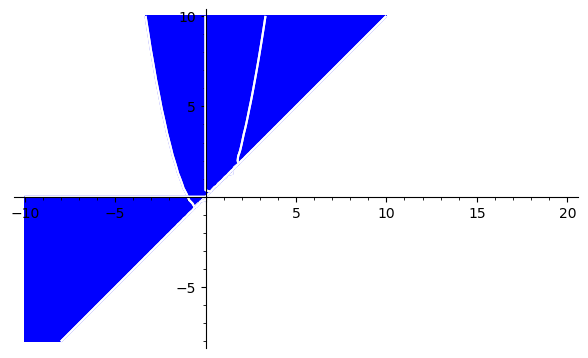
#Aby narysować (AuB)\C, wystarczy narysować A\C oraz B\C. A\C to zbiór punktów spełniających warunki
#definiujące zbiór A i niespełniających warunków definiujących zbiór C
var('x', 'y')
A_minus_C = region_plot([y >= x^2 - 1, x < y],(x,-10,20),(y,-8,10))
B_minus_C = region_plot([x*y > 0, x<y],(x,-10,20),(y,-8,10))
(A_minus_C+B_minus_C).show()
Suma i przekrój ciągu zbiorów#
Nauczyliśmy się już wyznaczać sumę i przekrój dla dwóch, trzech, czy ogólnie - dowolnej skończonej liczby zbiorów. Operacje te można jednak wykonać również dla ciągu zbiorów. Załóżmy, że \(A_1, A_2, \ldots, \) jest nieskończonym ciągiem zbiorów. Wtedy definiujemy:
Przykład#
Niech \(A_i = [\frac 1i, 1+\frac 1i]\) (przykładowo \(A_1 = [1, 2]\), \(A_2 = [\frac 12, \frac 32]\), …). Znajdź \(\bigcup_{i = 1}^{\infty} A_i\) oraz \(\bigcap_{i = 1}^{\infty} A_i\).
#Ten kod oblicza sumę i przekrój dla pierwszych n przedziałów przy zadanym n.
n = 100
suma_przedzialow = RealSet([1/1, 1+1/1])
for i in range(1, n):
suma_przedzialow.union(RealSet([1/i, 1+1/i]))
pretty_print(LatexExpr('\\bigcup_{i = 1}^{%d} A_i = '%(n)+str(suma_przedzialow)))
przekroj_przedzialow = RealSet([1/1, 1+1/1])
for i in range(1, n):
przekroj_przedzialow = przekroj_przedzialow.intersection(RealSet([1/i, 1+1/i]))
pretty_print(LatexExpr('\\bigcap_{i=1}^{%d} A_i = '%(n)+str(przekroj_przedzialow)))
# Ten kod służy do rysowania podzbiorów prostej rzeczywistej w zadanym kolorze i z zadanym podpisem.
# Przedziały narysujemy z różnym kolorem i wysokością, żeby rysunek był bardziej czytelny.
def narysuj_przedzial(realset, kolor='blue', tekst="", wysokosc = 0.1):
i = 0
wynik = text("", (0, 0))
try:
while (i>=0):
odcinek = realset.get_interval(i)
a, b = odcinek.lower(), odcinek.upper()
if a == b and odcinek.lower_closed() and odcinek.upper_closed():
wynik += circle((a, 0), wysokosc/2, fill=True, rgbcolor = kolor)
if i==0:
wynik += text(tekst, (a,2*wysokosc), color = 'black', fontsize = 10)
i += 1
else:
if a == -oo:
a = -4
lewy_koniec = text("", (0, 0))
else:
lewy_koniec = circle((a, 0), wysokosc/2, rgbcolor = kolor, fill = odcinek.lower_closed())
if b == oo:
b = 4
prawy_koniec = text("", (0, 0))
else:
prawy_koniec = circle((b, 0), wysokosc/2, rgbcolor = kolor, fill = odcinek.upper_closed())
wynik += polygon2d([(a,0), (a+wysokosc,wysokosc), (b-wysokosc,wysokosc), (b,0)], alpha=0.5, rgbcolor = kolor, edgecolor = 'black')+lewy_koniec+prawy_koniec
if i==0:
wynik += text(tekst, ((a+b)/2,2*wysokosc), color = 'black', fontsize = 10)
i+=1
except:
return wynik
def przekroj_przedzialow(n):
A = RealSet([1, 2])
C = narysuj_przedzial(A, kolor=(0.75, 0.85, 0.85), tekst="", wysokosc = 0.2)
for i in range(1, n):
A = RealSet([1/i, 1+1/i])
C += narysuj_przedzial(A, kolor=(0.75, 0.85 - i*0.01, 0.85), tekst="", wysokosc = max(0.2 - 0.01*i, 0.01))
return C
# Aplet rysujący przedziały.
@interact
def _(n = slider(0, 20)):
C = przekroj_przedzialow(n)
C.show()
przedzialy = [przekroj_przedzialow(3*n) + text("n = " + str(n), (0, 0.5)) for n in range(1, 6)]
# Wersja statyczna powyższego apletu.
g1=graphics_array(przedzialy,ncols=5)
g1.show(figsize=[10,10], ticks = [None, []])

Przykład#
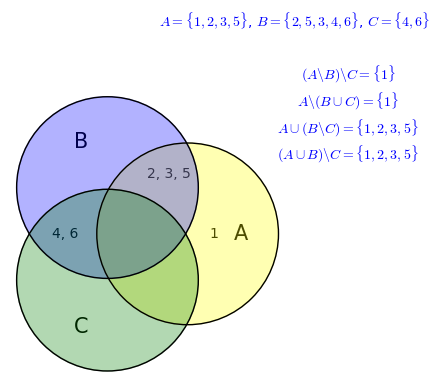
Sprawdź, korzystając z diagramów Venna, czy następujące równości są prawdziwe dla dowolnych zbiorów \(A\), \(B\), \(C\). W przeciwnym wypadku podaj przykład zbiorów \(A\), \(B\), \(C\), które nie spełniają danej równości.
(a) \((A \setminus B) \setminus C = A \setminus (B \cup C)\),
(b) \(A \cup (B \setminus C) = (A \cup B) \setminus C\).
Wskazówka: korzystając z poniższego apletu, możesz przetesować, czy dana równość zachodzi dla podanych przez Ciebie zbiorów.
# Aplet służący do rysowania diagramów Venna dla zadanych zbiorów.
# Funkcja służąca do odpowiedniej zamiany zmiennej typu Set na string.
def f(s, braces=True):
t = ', '.join(sorted(list(s)))
if braces: return '\\{' + t + '\\}'
return t
# Funkcja służąca do zmiany odpowiedniej zmiennej typu String na zmienną typu Set.
def g(s): return set(str(s).replace(',',' ').split())
# Funkcja rysująca diagramy Venna.
def diagramy_venna(A, B, C):
S = [g(A), g(B), g(C)]
A,B,C = S
AB = A & B
AC = A & C
BC = B & C
ABC = AB & C
A_minus_B = A.difference(B)
A_minus_B_minus_C = A_minus_B.difference(C)
B_suma_C = B.union(C)
A_minus_B_suma_C = A.difference(B_suma_C)
B_minus_C = B.difference(C)
A_suma_nawias_B_minus_C = A.union(B_minus_C)
A_suma_B = A.union(B)
A_suma_B_minus_C = A_suma_B.difference(C)
G = Graphics()
G += text('$(A \\backslash B)\\backslash C ='+(f(A_minus_B_minus_C)) +'$', (4, 3))
G += text("$A \\backslash (B \\cup C) = "+(f(A_minus_B_suma_C)) + '$', (4, 2.5))
G += text("$A \\cup (B \\backslash C) = "+(f(A_suma_nawias_B_minus_C)) + '$', (4, 2))
G += text("$(A \\cup B) \\backslash C = "+(f(A_suma_B_minus_C)) + '$', (4, 1.5))
centers = [(cos(n*2*pi/3), sin(n*2*pi/3)) for n in [0,1,2]]
scale = 1.7
clr = ['yellow', 'blue', 'green']
for i in range(len(S)):
G += circle(centers[i], scale, rgbcolor=clr[i],
fill=True, alpha=0.3)
for i in range(len(S)):
G += circle(centers[i], scale, rgbcolor='black')
# Plot what is in one but neither other
for i in range(len(S)):
C = set(S[i])
for j in range(1,len(S)):
C = C.difference(S[(i+j)%3])
G += text(f(C,braces=False), (1.5*centers[i][0],1.7*centers[i][1]), rgbcolor='black')
G += text(['A', 'B', 'C'][i], (2*centers[i][0],2*centers[i][1]), rgbcolor='black', fontsize = 15)
# Plot pairs of intersections
for i in range(len(S)):
C = (set(S[i]) & S[(i+1)%3]) - set(ABC)
Z = (1.3*cos(i*2*pi/3 + pi/3), 1.3*sin(i*2*pi/3 + pi/3))
G += text(f(C,braces=False), Z, rgbcolor='black')
# Plot intersection of all three
G += text(f(ABC,braces=False), (0,0), rgbcolor='black')
# Show it
return G
#Aplet interaktywny.
@interact
def _(A='1,2,3,5', B='2,5,3,4,6', C='4, 6'):
G = diagramy_venna(A, B, C)
G.show(aspect_ratio=1, axes=False)
grafika = diagramy_venna(A='1,2,3,5', B='2,5,3,4,6', C='4, 6') + text("$A=\\{1,2,3,5\\}$, $B=\\{2,5,3,4,6\\}$, $C=\\{4, 6\\}$", (3, 4))
#wersja statyczna apletu
grafika.show(aspect_ratio=1, axes=False)
Zadania do samodzielnego rozwiązania#
Przykład do samodzielnego rozwiązania#
Oblicz i narysuj \(A \cup B\), \(A \cap B\), \(A \setminus B\), \(B \setminus A\) dla \(A = [-\infty, 1] \cup \{ 2 \}\) B = \([0, 2] \cup \{ 3 \}\).
Przykład do samodzielnego rozwiązania#
Wypisz wszystkie dwuelementowe podzbiory zbioru \(A = \{ 1, \{1 \}, \{1, \{1 \}\}, \{ \{1 \} \} \}\).
Przykład do samodzielnego rozwiązania#
Niech:
Określ relacje pomiędzy zbiorami \(A\), \(B\), \(C\) (tzn. który ze zbiorów jest podzbiorem innego z tych zbiorów).
Przykład do samodzielnego rozwiązania#
Rozważmy następujące podzbiory płaszczyzny:
Narysuj zbiory \(B \cup (A \cap C)\) oraz \((A \setminus B) \cap C\).
Przykład do samodzielnego rozwiązania#
Czy dla dowolnych zbiorów \(A\), \(B\), \(C\) prawdziwe są równości:
(a) \(A \cap B = A \setminus (A \setminus B)\),
(b) \((A \setminus C) \cup B = A \cup B\)?
Uzasadnij za pomocą diagramów Venna lub podaj przykład zbiorów nie spełniających równości.