05. Teoria mnogości - część 2#

Tresci kształcenia: Podstawy teorii mnogości. Zbiory i operacje na zbiorach. Pojęcie zbioru, zbioru pustego, elementu, należenia, inkluzji. Podzbiory prostej rzeczywistej, przedziały, suma, przekrój, różnica zbiorów. Zbiory przeliczalne i nieprzeliczalne.

Efekty kształcenia: Student potrafi wykonać podstawowe operacje na zbiorach, określić ich przeliczalność.

Iloczyn kartezjański zbiorów#

Zajęcia te zaczniemy od przedstawienia jeszcze jednej operacji na zbiorach - iloczynu kartezjańskiego. Przed zdefiniowaniem tego pojęcia, musimy powiedzieć, czym jest para uporządkowana. Jest to kolekcja dwóch elementów, w której kolejność ma znaczenie. Innymi słowy dwie pary uporządkowane \((x_1, y_1)\) oraz \((x_2, y_2)\) są równe, jeżeli \(x_1 = x_2\) oraz \(y_1 = y_2\). Parę uporządkowaną dwóch liczb można przedstawić graficznie jako punkt na płaszczyźnie.

Definicja

Iloczynem kartezjańskim zbiorów A oraz B nazywamy zbiór:

\[ \{ (a, b) : a \in A, b \in B \}, \]

tzn. zbiór złożony z par uporządkowanych \((a, b)\), gdzie \(a \in A\), zaś \(b \in B\). Zbiór ten oznaczamy jako \(A \times B\).

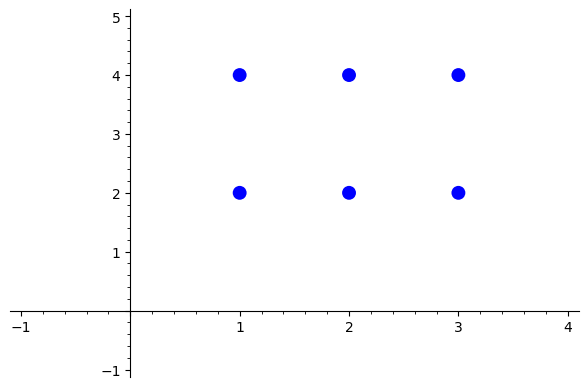
Przykład#

Zbiór \(\{ \color{blue}{1, 2, 3} \} \times \{ \color{green}{2, 4}\}\) ma sześć elementów. Są to pary \((\color{blue} 1, \color{green}2), (\color{blue} 1, \color{green}4), (\color{blue} 2, \color{green}2), (\color{blue} 2, \color{green}4), (\color{blue} 3, \color{green}2), (\color{blue} 3, \color{green}4)\). Możemy zatem przedstawić go graficznie na płaszczyźnie w następujący sposób:

#Rysujemy podane punkty.

from sage.plot.point import Point
P = point([(i, j) for i in range(1, 4) for j in [2, 4]], size=100)
P.show(xmin=-1, xmax=4, ymin=-1, ymax=5)

#Aby znaleźć iloczyn kartezjański dwóch zbiorów skończonych w Pythonie, można skorzystać z funkcji product z pakietu itertools.

import itertools
A = Set([1, 2, 3])
B = Set([2, 4])
AxB = Set(itertools.product(A, B))
print(AxB)

#Alternatywnie, można ręcznie utworzyć zbiór par uporządkowanych.
A_x_B = Set([(a, b) for a in A for b in B])
print(A_x_B)

{(2, 4), (1, 2), (3, 4), (2, 2), (3, 2), (1, 4)}
{(2, 4), (1, 2), (3, 4), (2, 2), (3, 2), (1, 4)}

Przykład#

Niech \(A = (1, 2] \cup \{ 3 \}\), zaś \(B = [2, 3)\). Narysuj na płaszczyźnie zbiór \(A \times B\).

#Rysujemy iloczyn kartezjański. Osobno rysujemy kwadrat bez krawędzi, a następnie dodajemy trzy odcinki (dwa boki kwadratu i jeden osobny odcinek)

kwadrat = polygon2d([[1,2], [1,3], [2, 3], [2,2]], fill=True, thickness=0, color=(0.75, 0.85, 0.85), edgecolor = 'black')
prawa_krawedz = line([(2,2), (2,3)], color = 'black', thickness = 4)
dolna_krawedz = line([(1,2), (2,2)], color = 'black', thickness = 4)
odcinek = line([(3,2), (3,3)], color = 'black', thickness = 4)
wierzcholek1 = circle((2, 2), 0.05, rgbcolor = 'black', fill = True)
wierzcholek2 = circle((1, 2), 0.05, fill = False, edgecolor='black')
wierzcholek3 = circle((1, 3), 0.05, fill = False, edgecolor='black')
wierzcholek4 = circle((2, 3), 0.05, fill = False, edgecolor='black')
wierzcholek5 = circle((3, 2), 0.05, fill = True, color = 'black', edgecolor='black')
wierzcholek6 = circle((3, 3), 0.05, fill = False, edgecolor='black')

(kwadrat+prawa_krawedz+dolna_krawedz+odcinek+wierzcholek1+wierzcholek2+wierzcholek3+wierzcholek4+wierzcholek5+wierzcholek6).show()

Moc zbiorów#

W drugiej części zajęć zajmiemy się mocą zbiorów, czyli intuicyjnie mówiąc, liczbą ich elementów. Moc zbioru \(A\) oznaczamy jako \(|A|\). Mamy na przykład \(|\{ 1, 2, 3 \}| = 3\). Jeżeli zbiory \(A\) oraz \(B\) są skończone, to \(|A \times B| = |A| \cdot |B|\). Przykładowo: \(|\{ 1, 2, 3 \} \times \{ 2, 4 \}| = 3 \cdot 2 = 6\) (patrz przykład wyżej).

Zasada włączeń i wyłączeń#

Załóżmy, że w restauracji 10 klientów zamówiło zupę, a 15 drugie danie. Zastanówmy się, ilu klientów może mieć w obecnej chwili restauracja? Możliwości są różne:

Z jednej strony, każdy klient, który zamówił zupę, mógł też zamówić drugie danie. W takim przypadku klientów jest 15.
Z drugiej strony mogło zdarzyć się tak, że żaden klient, którzy zamówił zupę, nie zamówił drugiego dania. Wtedy klientów byłoby \(10+15 = 25\).
Jest też możliwa każda pośrednia opcja - część klientów, która zamówiła zupę, zamówiła też drugie danie.

W każdym wypadku widzimy, że liczba klientów zależy od tego, ile klientów zamówiło i zupę, i drugie danie (czyli od przekroju zbiorów klientów zamawiających zupę i zbioru klientów zamawiających drugie danie). Z matematycznego punktu widzenia, dostajemy wzór:

\[ |A \cup B| = |A| + |B| - |A \cap B|, \]

zwany zasadą włączeń i wyłączeń dla dwóch zbiorów. Podobnie mówi się o zasadzie włączeń i wyłączeń dla trzech zbiorów:

\[ |A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |B \cap C| - |C \cap A| + |A \cap B \cap C|, \]

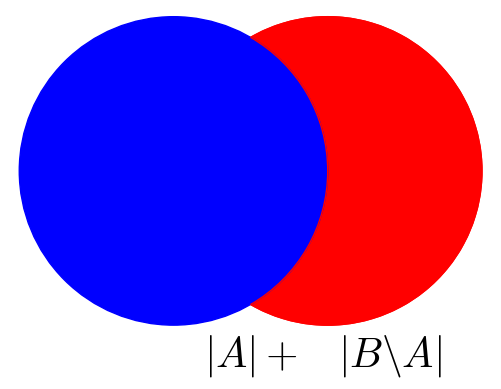
a także dla większej liczby zbiorów. Poniżej znajdziecie krótki dowód graficzny zasady włączeń i wyłączeń dla dwóch zbiorów.

#Kod rysujący diagramy Venna.
A1 = circle((0, 0), 1, color = 'blue', fill=True, edgecolor = 'black', thickness=3, linestyle='solid')
B1 = circle((1, 0), 1, color = 'blue', fill=True, alpha=1, edgecolor = 'black')

(A1+B1+ text(r'$|A \cup B| = $',(0.5,-1.2),rgbcolor='black', fontsize=30)).show(axes=false)

A = circle((0, 0), 1, color = 'blue', fill=True, alpha=1) + text(r'$|A| + $',(0.5,-1.2),rgbcolor='black', fontsize=30)
B = circle((1, 0), 1, color = 'red', fill=True, alpha=1, zorder=2)

BminA = arc((1,0), 1, sector=(pi+pi/3, pi+5*pi/3), color='red')+arc((0,0), 1, sector=(pi+2*pi/3,pi+4*pi/3), color='red')+text(r'$|B \backslash A|$',(1.4,-1.2),rgbcolor='black', fontsize=30)
(A+B+BminA).show(axes=false)

Przykład#

Ile jest liczb całkowitych dodatnich nie większych niż 10000 podzielnych co najmniej przez jedną z liczb: 2, 3 lub 5?

Rozwiązanie#

Niech \(A_2 = \{ x \in \mathbb Z_+ : x \le 10000, 2|x \}\), \(A_3 = \{ x \in \mathbb Z_+ : x \le 10000, 3|x \}\), \(A_5 = \{ x \in \mathbb Z_+ : x \le 10000, 5|x \}\) będą zbiorami liczb całkowitych dodatnich nie większych niż 10000 oraz podzielnych przez odpowiednio 2, 3 lub 5. Wtedy zbiór liczb podzielnych przez 2, 3 lub 5 to

\[ A_2 \cup A_3 \cup A_5. \]

Zauważmy, że:

\[ |A_2| = |\{ 2, 4, 6, 8, \ldots, 10000 \}| = 10000/2 = 5000. \]

Ponadto \(|A_2 \cap A_3|\) to zbiór liczb podzielnych przez \(2\) oraz przez \(3\), czyli przez \(2 \cdot 3 = 6\). Stąd: \(A_2 \cap A_3 = \{ 6, 12, 18, ... \}\). Zauważmy, że \(10000/6 \approx 1666,66\), zatem największą liczbą w tym zbiorze jest \(6 \cdot 1666 = 9996\) oraz \(|A_2 \cap A_3| = 1666\). Analogicznie zauważamy, że \(A_2 \cap A_3 \cap A_5 = \{ 30, 60, 90, \ldots \}\) oraz że największą liczbą w tym zbiorze jest \(30 \cdot 333\) (ponieważ \(10000/30 \approx 333,33\)). Stąd \(|A_2 \cap A_3 \cap A_5| = 333\).

W podobny sposób obliczamy, że \(|A_3| = 3333\), \(|A_5| = 2000\), \(|A_2 \cap A_5| = 1000\) oraz \(|A_3 \cap A_5| = 666\). Zatem korzystając z zasady włączeń i wyłączeń:

\[ |A_2 \cup A_3 \cup A_5| = |A_2| + |A_3| + |A_5| - |A_2 \cap A_3| - |A_2 \cap A_5| - |A_3 \cap A_5| + |A_2 \cap A_3 \cap A_5| = 5000 + 3333 + 2000 - 1666 - 1000 - 666 + 333 = 7334. \]

Nasz wynik sprawdzimy za pomocą prostego programu komputerowego.

# Zmienna podzielne_przez_2_3_5 zlicza ilość szukanych liczb.
podzielne_przez_2_3_5 = 0
for i in range(1, 10001):
    if i%2 == 0 or i%3 == 0 or i%5 == 0:
        podzielne_przez_2_3_5 += 1
print("Istnieje", podzielne_przez_2_3_5, "liczb całkowitych dodatnich nie większych niż 10000 i podzielnych co najmniej przez jedną z liczb 2, 3 lub 5.")

Istnieje 7334 liczb całkowitych dodatnich nie większych niż 10000 i podzielnych co najmniej przez jedną z liczb 2, 3 lub 5.

Przykład#

W sondażu dotyczącego umiejętności języka angielskiego wzięło udział 100 osób. Spośród nich:

28 osób zna język angielski,
33 osoby znają język niemiecki,
x osób zna język francuski,
16 osób zna język angielski i niemiecki,
13 osób zna język angielski i francuski,
y osób zna język niemiecki i francuski,
7 osób zna wszystkie trzy języki.

Czy to możliwe, że

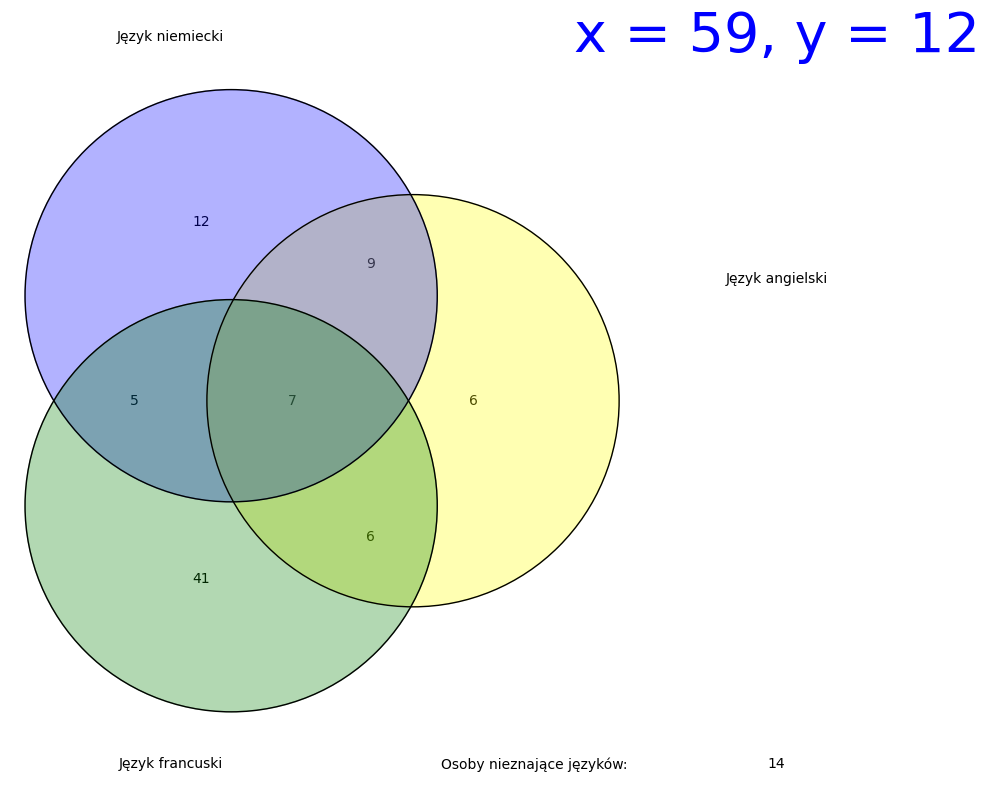
(a) x = 59, y = 12,

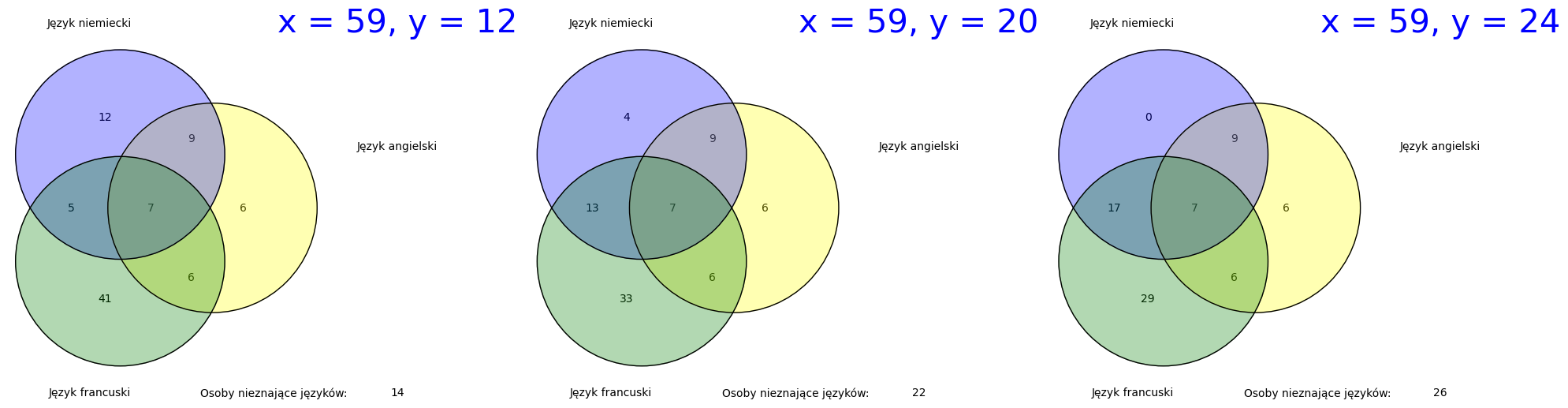
(b) x = 59, y = 25,

Wskazówka: skorzystaj z apletu poniżej. W podpunkcie (b), co dzieje się gdy \(x = 59\), zaś \(y = 12, 13, \ldots, 25\)? W podpunkcie (c), co dzieje się gdy \(y = 12\), zaś \(x = 59, \ldots, 75\)?

Rozwiązanie#

Zbiory osób znających język angielski, niemiecki lub francuski będziemy oznaczali odpowiednio literami \(A\), \(N\), \(F\).

(a) Zauważmy, że

\[ |A \setminus (N \cup F)| = |A| - |A \cap N| - |A \cap F| + |A \cap N \cap F| = 6 \]

\[ |N \setminus (A \cup F)| = |N| - |N \cap A| - |N \cap F| + |A \cap N \cap F| = 12 \]

\[ |F \setminus (N \cup A)| = |F| - |F \cap N| - |F \cap A| + |A \cap N \cap F| = 41 \]

-można zatem łatwo wskazać przykład, uzupełniając odpowiednie składowe diagramu Venna liczbami tak, jak pokazuje aplet poniżej.

(b) Mamy:

\[ |N \setminus (A \cup F)| = |N| - |N \cap A| - |N \cap F| + |A \cap N \cap F| = 33 - 25 - 16 + 7 = -1, \]

co daje sprzeczność.

\[ |A \cup N \cup F| = |A| + |N| + |F| - |A \cap N| - |N \cap F| - |A \cap F| + |A \cap N \cap F| = 28 + 33 + 75 -16-13 - 12 + 7 = 102. \]

Ale w sondażu brało udział sto osób! Sprzeczność kończy dowód!

def zbiory(Z, YZ):
    T = 100
    X = 28
    Y = 33
    XY = 16
    XZ = 13
    XYZ = 7
    
    centers = [(cos(n*2*pi/3), sin(n*2*pi/3)) for n in [0,1,2]]
    scale = 1.7
    clr = ['yellow', 'blue', 'green']
    G = Graphics()
    for i in range(3):
        G += circle(centers[i], scale, rgbcolor=clr[i],
             fill=True, alpha=0.3)
    for i in range(3):
        G += circle(centers[i], scale, rgbcolor='black')
   
    # etykiety
    G += text('Język angielski',(4,1),rgbcolor='black')
    G += text('Język niemiecki',(-1,3),rgbcolor='black')
    G += text('Język francuski',(-1,-3),rgbcolor='black')
   
    # przecięcia par zbiorów
    ZX=XZ-XYZ
    G += text(ZX, (1.3*cos(2*2*pi/3 + pi/3), 1.3*sin(2*2*pi/3 + pi/3)), rgbcolor='black')
    YX=XY-XYZ
    G += text(YX, (1.3*cos(0*2*pi/3 + pi/3), 1.3*sin(0*2*pi/3 + pi/3)), rgbcolor='black')
    ZY=YZ-XYZ
    G += text(ZY, (1.3*cos(1*2*pi/3 + pi/3), 1.3*sin(1*2*pi/3 + pi/3)), rgbcolor='black')
  
    # osoby znające tylko jeden język
    XX=X-ZX-YX-XYZ
    G += text(XX, (1.5*centers[0][0],1.7*centers[0][1]), rgbcolor='black')
    YY=Y-ZY-YX-XYZ
    G += text(YY, (1.5*centers[1][0],1.7*centers[1][1]), rgbcolor='black')
    ZZ=Z-ZY-ZX-XYZ
    G += text(ZZ, (1.5*centers[2][0],1.7*centers[2][1]), rgbcolor='black')
 
    # osoby znające trzy języki
    G += text(XYZ, (0,0), rgbcolor='black')
   
    # osoby nieznające języków
    C = T-XX-YY-ZZ-ZX-ZY-YX-XYZ
    G += text("Osoby nieznające języków:",(2,-3),rgbcolor='black')
    G += text(C,(4,-3),rgbcolor='black')
    
    # Czy wynik jest możliwy do uzyskania?
    if XYZ>XY or XYZ>XZ or XYZ>YZ or XY>X or XY>Y or XZ>X or XZ>Z or YZ>Y or YZ>Z or C<0 or XYZ<0 or XZ<0 or YZ<0 or XY<0 or X<0 or Y<0 or Z<0 or XX<0 or YY<0 or ZZ<0:
        print('Taka sytuacja jest niemożliwa!')
    else:
        
        return G
        
@interact
def _(x=slider([0..100],default=59,label='Francuski'),y=slider([0..100],default=12,label='Niemiecki i francuski')):
    G = zbiory(Z = x, YZ = y)
    G.show(aspect_ratio=1, axes=False)

#Przykład dla konkretnych wartości.
#
zbiory_a = zbiory(Z = 59, YZ = 12) + text("x = 59, y = 12", (4, 3), fontsize = 40)

zbiory_b = [zbiory(Z = 59, YZ = 12) + text("x = 59, y = 12", (4, 3), fontsize = 30)]
zbiory_b.append(zbiory(Z = 59, YZ = 20) + text("x = 59, y = 20", (4, 3), fontsize = 30))
zbiory_b.append(zbiory(Z = 59, YZ = 24) + text("x = 59, y = 24", (4, 3), fontsize = 30))

zbiory_c = [zbiory(Z = 60, YZ = 12) + text("x = 60, y = 12", (4, 3), fontsize = 30)]
zbiory_c.append(zbiory(Z = 65, YZ = 12) + text("x = 65, y = 12", (4, 3), fontsize = 30))
zbiory_c.append(zbiory(Z = 73, YZ = 12) + text("x = 73, y = 12", (4, 3), fontsize = 30))

#Narysujemy przykładowe ustawienia x, y dla wartości ważnych w odpowiednich podpunktach.
zbiory_a.show(figsize=[10,10], axes=False)
g1=graphics_array(zbiory_b,ncols=3)
g1.show(figsize=[20,20], axes = False, ymin = -3, ymax = 3)

g2=graphics_array(zbiory_c,ncols=3)
g2.show(figsize=[20,20], axes = False, ymin = -3, ymax = 3)

Przykład#

Ile elementów ma zbiór

\[ (\{ -2, -1, \ldots, 2 \} \times \{ -3, -2, \ldots, 2 \}) \cup (\{ 1, 2, 3, 4 \} \times \{ 0, 1, 2, 3, 4 \})? \]

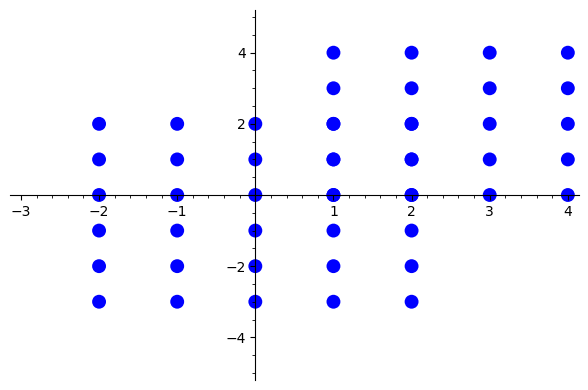
Niech \(A = \{ -2, -1, \ldots, 2 \} \times \{ -3, -2, \ldots, 2 \}\), zaś \(B = \{ 1, 2, 3, 4 \} \times \{ 0, 1, 2, 3, 4 \}\). Wtedy \(|A| = 5 \cdot 6 = 30\) oraz \(|B| = 4 \cdot 5 = 20\). Ponadto \(A \cap B = \{ 1, 2 \} \times \{ 0, 1, 2 \}\). Stąd:

\[ |A \cup B| = |A| + |B| - |A \cap B| = 30 + 20 - 6 = 44. \]

# A to zbiór {-2, ..., 2}x{-3, ..., 2}, zaś B to zbiór {1, ..., 4}x{0, ..., 4}.
#Podany program podaje moc ich sumy.
A = Set([(i, j) for i in range(-2, 3) for j in range(-3, 3)])
B = Set([(i, j) for i in range(1, 5) for j in range(0, 5)])
S = A.union(B)
print(S.cardinality())

# Narysujmy rozważany zbiór.

from sage.plot.point import Point
P = point([(i, j) for i in range(-2, 3) for j in range(-3, 3)], size=100)
P += point([(i, j) for i in range(1, 5) for j in range(0, 5)], size=100)
P.show(xmin=-3, xmax=4, ymin=-5, ymax=5)

Zbiory przeliczalne i nieprzeliczalne#

Oprócz zbiorów skończonych mamy również zbiory nieskończone. Co ciekawe, okazuje się, że istnieją “większe” i “mniejsze” zbiory nieskończone!

Definicja

Mówimy, że zbiór \(A\) jest przeliczalny, jeżeli jego elementy można ustawić w ciąg (skończony lub nie).

Przykład#

Zbiór liczb całkowitych jest przeliczalny, bo jego elementy można ustawić w ciąg w następujący sposób:

\[ 0, -1, 1, -2, 2, -3, 3, \ldots. \]

Przykład#

Zbiór liczb parzystych jest przeliczalny, bo jego elementy można ustawić w ciąg w następujący sposób:

\[ 0, -2, 2, -4, 4, -6, 6, \ldots. \]

Przykład#

Okazuje się, że również zbiór liczb wymiernych jest przeliczalny. Aby to pokazać, utwórzmy tabelę, w której na przecięciu \(i\)-tego wiersza oraz j-tej kolumny stoi liczba wymierna \(\frac ij\) dla \(i, j = 1, 2, \ldots\). Następnie przejdźmy tabelę tak, jak wskazują strzałki na poniższym rysunku:

# Kod rysujący tabelę z liczbami wymiernymi.

A = text("", (-1, -1))
for i in range(1, 9):
    for j in range(1, 9):
        if GCD(i, j) == 1:
            A += text(str(i)+"/"+str(j), (i, j), color = 'black')
        else:
            A += text(str(i)+"/"+str(j), (i, j), color = 'red')
        if i>=2 and (i+j)%2 == 1:
            A += arrow((i, j), (i-1, j+1), arrowshorten = 20, arrowsize = 2)
        if i>=2 and (i+j)%2 == 0:
            A += arrow((i-1, j+1), (i, j), arrowshorten = 20, arrowsize = 2)
        if i == 1 and j >=2 and j%2 == 0:
            A += arrow((i, j), (i, j+1), arrowshorten = 10, arrowsize = 2)
        if j == 1 and i%2 == 1:
            A += arrow((i, j), (i+1, j), arrowshorten = 20, arrowsize = 2)
        if i == 1 and j == 1:
            A += arrow((1,1), (2, 1), arrowshorten = 20, arrowsize = 2)
A.show(axes = false, aspect_ratio = 0.5)

W ten sposób uzyskaliśmy ciąg zawierający wszystkie dodatnie liczby wymierne - jego pierwsze wyrazy to:

\[ \frac 11, \frac 21, \frac 12, \frac 13, \frac 22, \frac 31, \ldots. \]

Każda liczba powtarza się w tym ciągu nieskończenie wiele razy (bo np. \(\frac 11 = \frac 22 = \frac 33 = \ldots = 1\)), ale to nie problem. Możemy przecież wykreślić powtarzające się elementy z ciągu (zaznaczyliśmy wykreślane elementy w tabeli na czerwono). Oto pierwsze wyrazy uzyskanego w ten sposób ciągu:

\[ 1, 2, \frac 12, \frac 13, 3, 4, \frac 32, \frac 23, \frac 14, \frac 15, 5, \ldots \]

Przykład#

Okazuje się, że nie każdy zbiór jest przeliczalny. Naszkicujemy teraz dowód faktu, że odcinek \((0, 1)\) jest nieprzeliczalny. Jest to tak zwana metoda przekątniowa Cantora. Załóżmy nie wprost, że udało nam się ustawić wszystkie liczby z przedziału \((0, 1)\) w ciąg \(a_1, a_2, a_3, \ldots\). Rozważmy rozwinięcia dziesiętne liczb w ciągu. Jeżeli któraś z liczb na skończone rozwinięcie, dopiszmy nieskończenie wiele zer. Utwórzmy nową liczbę \(a \in (0, 1)\) w następujący sposób:

jej pierwszą cyfrą po przecinku jest dowolna cyfra różna od pierwszej cyfry liczby \(a_1\) oraz od cyfry \(9\),
jej drugą cyfrą po przecinku jest dowolna cyfra różna od drugiej cyfry liczby \(a_2\) oraz od cyfry \(9\),
jej trzecią cyfrą po przecinku jest dowolna cyfra różna od trzeciej cyfry liczby \(a_3\) oraz od cyfry \(9\),

i tak dalej. Ponieważ w zapisie liczby \(a\) nie występuje cyfra \(9\), ma ona jednoznaczny zapis dziesiętny. Liczba \(a\) nie może występować w tym ciągu, ponieważ różni się przynajmniej jedną cyfrą z każdą liczbą w ciągu. Dla przykładu, jeżeli liczby w ciągu wyglądają następująco:

\[ a_1 = 0,{ \color{red}7}2914153946100800927239825167455700423140031213160 \ldots \]

\[ a_2 = 0,0{ \color{red}5}703499398506417803443814288344130324488652422423 \ldots \]

\[ a_3 = 0,47{ \color{red}2}60549464937888464857234409059404878273865237408 \ldots \]

\[ a_4 = 0,848{ \color{red}6}4489486821992621001453107232909353022794063046 \ldots \]

\[ a_5 = 0,1245{ \color{red}0}781586846597827135854060075612975208532014674 \ldots \]

\[ a_6 = 0,68053{ \color{red}0}68505231436803593524867561561641622148807372 \ldots \]

\[ a_7 = 0,643680{ \color{red}6}9780985694325900682868134090738072367639157 \ldots \]

\[ a_8 = 0,3979407{ \color{red}2}202696262936617027211195299172355122743815 \ldots \]

\[ a_9 = 0,94284775{ \color{red}6}78362930147489518107254361959917702779744 \ldots \]

\[ a_{10} = 0,060679495{ \color{red}9}7097863119018446677681120880732956824642 \ldots \]

to możemy przyjąć \(a = 0, 8637117370 \ldots\). Przykład ten ilustruje przy okazji, czemu argument ten nazywa się metodą przekątniową.

Zauważmy, że nieprzeliczalny jest zatem również dowolny zbiór zawierający przedział \((0, 1)\), np. \([0, 1]\) lub \(\mathbb R\). Istotnie, gdyby np. wszystkie liczby rzeczywiste można było ustawić w ciąg, to po wykreśleniu liczb spoza przedziału \((0, 1)\), otrzymalibyśmy ciąg elementów \((0, 1)\) - sprzeczność!

Uwaga: pojęcie przeliczalności ma duże znaczenie w algorytmice. Przykładowo, okazuje się, że zbiór programów w danym języku programowania jest przeliczalny. Zbiór funkcji \(f : \mathbb N \to \mathbb N\) jest jednak nieprzeliczalny. Zatem nie każdą funkcję można zapisać za pomocą programu komputerowego!

Zadania do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Narysuj zbiory:

\(\{0, 2, 4\} \times \{ 1, 3, 5 \}\),
\(\bigg((1, 2] \cup \{3 \} \bigg) \times \bigg( \{ 1 \} \cup [2, 4) \bigg)\),
\((1, 2] \times \{ 1, 3, 5 \}\),
\((- \infty, 0) \times (1, 4]\).

Przykład do samodzielnego rozwiązania#

Ile jest liczb całkowitych dodatnich nie większych niż 8000 jest podzielnych co najmniej przez jedną z liczb: 3, 5 lub 7?

Przykład do samodzielnego rozwiązania#

Ile elementów przebiega pętla zagnieżdżona:

for i = 1 to 5:
        for j = 8 to 20:
            ...

a ile dwie osobne pętle:

for i = 1 to 5:
    ...
for j = 8 to 20:
    ...

Przykład do samodzielnego rozwiązania#

Liczba \(t \in \mathbb Z_+\) jest większa od 1. Wiadomo, że zbiór:

\[ (\{ x \in \mathbb Z : x^2 <10 \} \times \{ x \in \mathbb Z : x^2 \le 16 \}) \cup (\{ 2, 3, 4, 5 \} \times \{ 1, 2, 3, \ldots t \}) \]

ma 79 elementów. Znajdź \(t\).

Przykład do samodzielnego rozwiązania#

Czy zbiór liczb nieparzystych jest przeliczalny?

Przykład do samodzielnego rozwiązania#

Czy zbiór wszystkich funkcji liniowych o współczynnikach wymiernych jest przeliczalny?

Przykład do samodzielnego rozwiązania#

Czy zbiór \([0, 1] \times [0, 1]\) jest przeliczalny?

Przykład do samodzielnego rozwiązania#

Czy zbiór \(\mathbb N \times \mathbb N\) jest przeliczalny?

Przykład do samodzielnego rozwiązania#

Czy zbiór ciągów binarnych skończonej długości jest przeliczalny? A co ze zbiorem ciągów binarnych nieskończonej długości?

Uwaga: ciąg binarny to ciąg złożony z samych zer i jedynek, np. \((0, 1, 0, 0, 0, 1, 1, 0)\).

Wstęp do matematyki 06-DPMALI0

05. Teoria mnogości - część 2

Contents

05. Teoria mnogości - część 2#

Iloczyn kartezjański zbiorów#

Przykład#

Przykład#

Moc zbiorów#

Zasada włączeń i wyłączeń#

Przykład#

Rozwiązanie#

Przykład#

Rozwiązanie#

Przykład#

Zbiory przeliczalne i nieprzeliczalne#

Przykład#

Przykład#

Przykład#

Przykład#

Zadania do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#

Przykład do samodzielnego rozwiązania#