13. Rekurencja 2.#

Treści kształcenia. Ciągi zadane rekurencyjnie w informatyce. Granice ciągów, algorytmy obliczania granic (problem zbieżności). Interpretacja geometryczna (programy), obliczanie granic, punkty skupienia ciągów.

Efekty kształcenia: Student potrafi operować ciągami rekurencyjnymi, badać ich zbieżność i granice. Potrafi określić podstawowe wady i zalety takich ciągów w zastosowaniach informatycznych.

Badamy ciągi rekurencyjne. Tak dla przypomnienia: ciąg to funkcja określona na liczbach naturalnych}. Tzw. ‘’ciągi skończone’’ nie powinny być traktowane jako ‘’ciągi’’ w sensie przez nas badanym. Zamiast ‘’liczby \(a,b,c\) tworzą ciąg…’’ raczej powinno się mówić ‘’liczby \(a,b,c\) są (pierwszymi) wyrazami ciągu …’’.

a) Od wzoru ogólnego do rekurencji.

Stosunkowo łatwo (?) można wyznaczyć wzór rekurencyjny ciągu, gdy znany jest jego wzór ogólny.

Przykład 1. Niech dany będzie ciąg o wyrazie ogólnym

\[ a_n = \frac {n(n+2)}{3} . \]

Wyznaczyć jego wzór rekurencyjny.

Rozwiązanie.

Wyznaczmy najpierw pierwszy wyraz tego ciągu. łatwo sprawdzić, że \(a_1 = 1\).

Wiemy także, że \(a_{n+1} = \frac {(n+1)(n+3)}{3}\). Stąd możemy policzyć różnicę wyrazów następnego i poprzedniego:

\[ a_{n+1} -a_n= \frac {(n+1)(n+3)}{3} - \frac {n(n+2)}{3}= \frac {n^2+n+3n+3-n^2-2n}{3} = \frac {2n+3}{3}, \]

stąd zaś wynika, że \(a_{n+1} = a_n + \frac{2n+3}{3}\). Ostatecznie więc zapisujemy wzór rekurencyjny ciągu w oparciu o jego pierwszy wyraz:

\[ a_1 = 1 \qquad a_{n+1} = a_n + \frac{2n+3}{3} \qquad \forall n \ge 1 . \]

Przykład 2.

Rozpatrzmy ciąg

\[ a_n = (n-5)\cdot (n+5) \]

Wyznaczyć jego wzór rekurencyjny.

Rozwiązanie.

Rozpoczniemy od pierwszego wyrazu: \(a_1 = (-4)\cdot 6 = -24\). Zauważmy, że \(a_n = n^2 -25\). Teraz badamy wyraz \(a_{n+1}\):

\[ a_{n+1} = (n+1-5)\cdot (n+1+5) = (n-4)\cdot(n+6) = n^2 +2n - 24 = (n^2 -25) +2n +1 = a_n +2n +1. \]

Przykład 3. (samodzielne) Rozpatrzmy ciąg

\[ a_n = \frac{1}{n+4} . \]

Wyznaczyć jego wzór rekurencyjny.

Przykład 4. Rozpatrzmy ciąg Lucasa

\[ a_n = 2^n + (-1)^n \qquad (n \geq 0) . \]

Wyznaczymy jego wzór rekurencyjny.

Rozwiązanie.

Pierwsze wyrazy to \(a_0 = 2\), \(a_1 = 1\). Mamy

\[ a_{n+1} = 2^{n+1} + (-1)^{n+1} = 2\cdot 2^n + (-1)\cdot (-1)^2 = 2\cdot 2^n + (-1)\cdot (-1)^n + 2\cdot (-1)^n - 2\cdot (-1)^n = 2\cdot \left( 2^n + (-1)^n \right) - 3\cdot (-1)^n = 2 \cdot a_n - 3\cdot (-1)^n . \]

Czyli wzór rekurencyjny to:

\[ a_0 = 2 \ , \ a_1 = 1 \ , \ a_{n+1} = 2a_n - 3\cdot (-1)^n \]

b) Od rekurencji do wzoru ogólnego.

‘’Algorytmy rekurencyjne są szczególnie odpowiednie, gdy podstawowy problem lub dane, które mają być przetwarzane są zdefiniowane w kategoriach rekurencyjnych. Nie oznacza to jednak, że takie rekurencyjne definicje gwarantują nalepszą efektywność algorytmu rekurencyjnego w rozwiązania problemu. Takie niewłaściwe przykłady były główną przyczyną powstania pewnej niechęci do stosowania rekurencji w programowaniu oraz utożsamiania rekurencji z nieefektywnością [N. Wirth].’’

Są więc sytuacje, gdy warto rozważyć przejście od rekurencji do wzoru ogólnego. A teraz dość trudny, ale klasyczny przykład.

Ciąg Fibonacci’ego. Wzór Bineta. A teraz problem uzyskiwania wzoru ogólnego na przykładzie ciągu Fibonacci’ego: 0, 1, 1, 2, 3, 5, 8, 13, 21,…

Wzór Bineta to jawny wzór na \(n\)-ty wyraz ciągu Fibonacciego podany w 1843 r. przez Jacques Philippe Marie Bineta możemy otrzymać, korzystając z pewnej formalnej metody (tzw. funkcji tworzących). Od razu uprzedzimy - podamy też póżniej inną, efektywną metodę ogólną dla rekurencji liniowych, a ten ciąg zbadamy ponownie tę metodą (nie jest jednak niezbędna - jak widać).

Niech dany będzie ciąg Fibonacciego \((f_n)\):

\[ f_0 = 1 \ , \ f_1 = 1 \ , \ f_{n+2} = f_{n+1} + f_n . \]

def F(n):
    F = []
    F.append(0)
    F.append(1)
    for i in range(2,n+1):
        F.append(F[i-1]+F[i-2])

    return F

F(10)

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55]

Ciąg Fibonacci’ego jest ciekawym obiektem i ma interesujące zastosowania - np.
,,Miniatury Matematyczne’’ tom 43, Ł. Mentzen, M.K. Mentzen, ,,Ciąg Fibonacciego’’, czy tom 31 ‘’MM” - A. Sendlewski ,,Zliczanie rekurencyjne’’.

Tworzymy funkcję \(s\):

\[ s(x)=\sum_{n=0}^\infty f_n \cdot x^n. \]

Podstawiając \(f_n = f_{n-1} + f_{n-2},\) otrzymujemy:

\[ s(x) = 1 + x + \sum_{n=2}^\infty \left( f_{n-2} + f_{n-1}\right) x^n \]

\[ = 1 + x + x^2 \sum_{n=2}^\infty f_{n-2} x^{n-2} + x \sum_{n=2}^\infty f_{n-1} x^{n-1} \]

\[ = 1 + x + x^2 s(x) + x (s(x)-1) = 1 + x s(x) + x^2 s(x). \]

W szczególności:

\[ s(x) = \frac{1}{1 - x - x^2}. \]

Ponieważ wielomian \(1-x-x^2\) ma dwa pierwiastki \(x_1=\frac{-\sqrt5-1}{2} , x_2=\frac{\sqrt5-1}{2}\) (proszę sprawdzić!),
to wyrażenie \(\frac{1}{1 - x - x^2}\) można przedstawić w postaci (rozkład na ułamki proste - proszę powtórzyć!):

\[ \frac{1}{1 - x - x^2} = \frac{A}{(1-ax)} + \frac{B}{(1-bx)}, \]

gdzie: \(a=\frac{1 + \sqrt{5}}{2},\) \(b=\frac{1 - \sqrt{5}}{2},\) \(A=\frac{a}{a-b},\) \(B=\frac{-b}{a-b}.\)

Wówczas:

\[ s(x)=A \sum_{n=0}^\infty a^n x^n + B \sum_{n=0}^\infty b^n x^n = \sum_{n=0}^\infty \frac{(a^{n+1} - b^{n+1})}{(a-b)}x^n, \]

a stąd:

\[ f_n = \frac{(a^{n+1} - b^{n+1})}{(a-b)}. \]

\[ F_n = \frac{1}{\sqrt 5}\left(\frac{1 + \sqrt 5}{2}\right)^n - \frac{1}{\sqrt 5}\left(\frac{1 - \sqrt 5}{2}\right)^n. \]

Mamy więc wyraz ogólny ciągu Fibonacci’ego. A właściwie dlaczego taka metoda? Pokażemy to także w nieco bardziej ogólnym przypadku: jak to zrobić w przypadku rekurencji liniowej.

Ale najpierw inny problem.

Zbieżność ciągu rekurencyjnego.

Skoro klasyczną metodą definiowania ciągów jest rekurencja (zwłaszcza w informatyce!): definiujemy kolejne wyrazy w oparciu o znajomość poprzednich (jak już wiemy: niekoniecznie jednego wyrazu). To - niestety - prowadzi do poważnego problemu: jak zbadać zbieżność ciągu zadanego rekurencyjnie, dla którego nie znamy jego wzoru ogólnego?

I tu widoczna jest przydatność twierdzeń o ciągach zbieżnych. Podstawowe narzędzie to twierdzenie o ciągach monotonicznych i ograniczonych. Przypomnijmy kluczowe własności w badaniu zbieżności ciągów rekurencyjnych:

Ciąg \((a_n)\) nazywamy ograniczonym, gdy

\[ {\exists}_{M > 0} \quad {\forall}_{n\in {\mathbb{N}}} \quad | a_n | < M . \]

W przypadku gdy \( {\exists}_{M_1}\) \({\forall}_{n\in\Bbb N}\) \(a_n\le M_1\) ciąg \((a_n)\) nazywamy ograniczonym z góry, natomiast w przypadku gdy \( {\exists}_{M_2}\) \({\forall}_{n\in \Bbb N}\) \(M_2\le a_n\) ciąg \((a_n)\) nazywamy ograniczonym z dołu.

Ciąg \((a_n)\) nazywamy monotonicznym jeżeli spełnia jeden z następujących warunków:

\[ {\forall}_{n\in \Bbb N} \quad a_n < a_{n+1}\ , \quad\quad\text {jest to ciąg rosnący} , \]

\[ {\forall}_{n\in \Bbb N} \quad a_n > a_{n+1} , \quad \quad\text {jest to ciąg malejący} , \]

\[ {\forall}_{n\in \Bbb N} \quad a_n\le a_{n+1} , \quad \quad\text {jest to ciąg niemalejący} , \]

\[ {\forall}_{n\in \Bbb N} \quad a_n\ge a_{n+1} , \quad\quad \text {jest to ciąg nierosnący} . \]

O ciągach spełniających pierwsze dwa warunki mówimy, że są ściśle monotoniczne. Warto zauważyć, że zakresy pojęć ciągów monotonicznych oraz ograniczonych przecinają się, tzn. istnieją ciągi które są ograniczone, ciągi które są monotoniczne oraz takie ciągi, które są równocześnie ograniczone i monotoniczne.

Zadania. Sprawdź, czy dane ciągi są monotoniczne:

(a)

\[ a_n = \sqrt{ n + 3} - \sqrt{ n+2} , \]

(b)

\[ a_n = \frac{n}{n^2 + 1} , \]

(c)

\[ a_n = \frac{n!}{n^n}. \]

Twierdzenie. Ciąg monotoniczny i ograniczony jest zbieżny.

(a) Jeżeli ciąg \((a_n)\) jest niemalejący i ograniczony z góry to jest zbieżny i wówczas

\[ \lim_{n\to\infty}a_n=\sup_{n} a_n \ . \]

(b) Jeżeli ciąg \((a_n)\) jest nierosnący i ograniczony z dołu to jest zbieżny i wówczas

\[ \lim_{n\to\infty}a_n=\inf_n a_n \ . \]

Obliczanie granic ciągów rekurencyjnych. Jeżeli ciąg rekurencyjny jest zbieżny (a mieliśmy różne przykłady), to kolejne pytanie brzmi: jak obliczyć jego granicę?

Przykład 1. Prosty przykład ciągu rekurencyjnego do zbadania:

\[ a_1 = 0 \ , \ 2 \cdot a_{n+1} = \left( a_n^2 + (1 - \frac{1}{n}) \right) \quad (n > 1). \]

Najpierw problem zbieżności tego ciągu: wystarczy wykazać, że jest monotoniczny i ograniczony. Przede wszystkim widoczne jest, że wyrazy są nieujemne i mniejsze niż 2. Ta ostatnia uwaga wynika z faktu, że \(1 - \frac{1}{n} < 1\) oraz że suma liczb (\(a_n^2\) oraz \(1-\frac{1}{n}\)) mniejszych niż 1 jest mniejsza niż 2. Formalny dowód: indukcja matematyczna!

Poza tym ciąg jest rosnący, ale ten dowód wymaga trochę starań. Przede wszystkim mamy

\[ a_{n+1} - a_n = \frac{1}{2} a_n^2 - a_n + 1 - \frac{1}{2n} = \frac{1}{2}\left( a_n - 1 \right)^2 - \frac{1}{2n} . \]

A ponieważ \(0 \leq a_n < 1\), to \(0 \leq \left( a_n - 1 \right)^2 < \frac{1}{2}\), a więc \(a_{n+1} - a_n > 0\) dla \(n > 1\).

Warto dodać, że nieco później (na analizie matematycznej) poznamy też inne (prostsze) metody badania monotoniczności takich ciągów.

I teraz kluczowe: jeżeli ciąg jest zbieżny (powiedzmy do granicy \(a\), to \(a_{n+1}\) też jest zbieżny do \(a\) (to własność ciągów zbieżnych) i stąd przechodząc obustronnie do granicy z \(n \to \infty\) (tak formalnie to zastosowanie twierdzenia o 3 ciągach):

\[ 2 \cdot a_{n+1} \leq \left( a_n^2 + (1 - \frac{1}{n}) \right) \leq 2 \cdot a_{n+1} \]

uzyskujemy:

\[ 2a = a^2 + 1 , \]

a więc \(a^2 - 2a + 1 = 0\), czyli \(a = 1\) lub \(a = -1\). Ale wszystkie wyrazy są nieujemne, więc ostatecznie pozostaje tylko jedna możliwość \(a = 1\).

Przykład 2. Określmy ciąg wzorem rekurencyjnym:

\[ a_1=1 \ , \ a_{n+1}=\sqrt {2+a_n} . \]

Sprawdzimy czy ten ciąg jest zbieżny i obliczyć jego granicę.

Rozwiązanie. Symulacja komputerowa sugeruje zbieżność, ale - to nie dowód…

x = RealField(25)(1)
for i in range(0,21):
    print("%s %s"%(i,x))
    x = sqrt(2+x)

Skorzystamy teraz z twierdzenia o ciągach monotonicznych i ograniczonych. Ciąg ten jest ograniczony z góry przez 2 (co można łatwo wykazać metodą indukcji zupełnej) oraz rosnący, gdyż

\[ a_{n+1}-a_n = \sqrt {2+a_n}-a_n =\frac {(\sqrt {2+a_n}-a_n)(\sqrt {2+a_n}+a_n)} {\sqrt {2+a_n}+a_n}= \]

\[ =\frac {2+a_n-a_n^2}{\sqrt {2+a_n}+a_n}=\frac {-(a_n+1)(a_n-2)}{\sqrt {2+a_n}+a_n}\ge 0 \]

(wykorzystaliśmy tu fakt, że \(1\le a_n\le 2\)). Można też inaczej: skoro wiemy o ograniczoności z góry wyrazów ciągu przez 2, to

\[ 2+a_n \ge a_n+a_n = 2a_n \ge a_n\cdot a_n = a_n^2 , \]

czyli

\[ a_{n} \le \sqrt{2+a_n} = a_{n+1} . \]

Jako ciąg monotoniczny i ograniczony jest więc zbieżny. Jego granicę oznaczmy przez \(a\).

Uwaga: skoro wiemy, że jest zbieżny, to możemy już zrobić symulację na komputerze.

def g(n):
    if n==1:
        return 1
    else:
        return sqrt(2+g(n-1))
    
list_plot([g(k) for k in range(2,36)],figsize=[3,3])

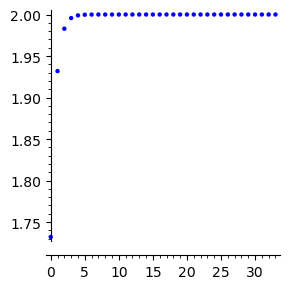
Oczywiście (a właściwie dlaczego??) ciąg \((a_{n+1})\) jest również zbieżny do \(a\) i stąd:

\[ a_{n+1} =\sqrt {2+a_n} \]

\[ a=\sqrt {2+a}. \]

Mamy więc kolejno: \(a=\sqrt {2+a}\), \(a^2=2+a\), \(a^2-a-2=0\), czyli \(a_1=2\)
oraz \(a_2=-1\), który odpada, gdyż \(a_n\ge 0\). Ostatnie równanie ma dwa pierwiastki. Ostatecznie \( \lim_{n\to\infty}a_n=2\). Jest to zgodne z naszymi oczekiwaniami po wykonaniu symulacji.

Podkreślmy tu jeszcze konieczność wykazania istnienia granicy ciągu, zanim zaczynamy ją obliczać.

Przykład 3. Ciąg rekurencyjny oczywiście nie musi być zbieżny (por. wcześniejszy przykład o pozornej zbieżności). Ale nawet niezbyt skomplikowane i ograniczone ciągi rekurencyjne nie muszą być zbieżne.

Określmy ciąg wzorem rekurencyjnym:

\[ a_1=0 \ , \ a_{n+1}=\sqrt {2-a_n^2} . \]

Sprawdzimy czy ten ciąg jest zbieżny. Rozpoczniemy od wyliczenia kilku wyrazów ciągu: \(a_1 = 0\), \(a_2 = \sqrt{2 - 0^2} = \sqrt{2}\), \(a_3 = \sqrt{2 - (\sqrt{2})^2} = 0\), \(a_4 = \sqrt{2 - 0^2}\), … Ciąg nie jest monotoniczny (choć ograniczony), a można wykazać (indukcja!)

\[ a_{2k} = 0 \ , \ a_{2k+1} = \sqrt{2} \quad (k \ge 0). \]

Ciąg rekurencyjny nie jest zbieżny (ma 2 punkty skupienia).

A teraz dobry moment, aby zauważyć, że zbieżność ciągu rekurencyjnego może być zależna od początkowych wyrazów! Pozostawmy bez zmian wzór rekurencyjny z tego zadania, ale zmieńmy pierwszy wyraz:

\[ a_1= 1 , a_{n+1}=\sqrt {2-a_n^2} . \]

Tym razem mamy więc: \(a_1 = 1\), \(a_2 = \sqrt{2 - 1^2} = 1\), \(a_3 = \sqrt{2 - 1^2} = 1\), \(a_4 = \sqrt{2 - 1^2} = 1\), … Ciąg jest stały! A więc zbieżny.

Przykład 4.

Niech \(a_0 = 1\), \(b_0 = x > 0\). Definiujemy

\[ a_{n+1} = \frac{2 a_n\cdot b_n}{a_n + b_n} , \]

\[ b_{n+1} = \frac{a_n + b_n}{2} . \]

Sprawdzić, że granice obu ciągów są równe i wynoszą \(\sqrt{x} = \sup_{n \in {\mathbb{N}}} \left\{ a_n \right\} = \inf_{n \in {\mathbb{N}}} \left\{ b_n \right\}\).

Rozwiązanie. Przede wszystkim trzeba zauważyć, że to ciągi średnich: \(b_{n+1}\) jest średnią arytmetyczną liczb \(a_n\) i \(b_n\), a \(a_{n+1}\) ich średnią harmoniczną. Załóżmy, że \(x> 1\) (przypadek \(x < 1\) jest analogiczny i pozostawiamy go do {\em samodzielnego} sprawdzenia).

Przypomnijmy nierówność Cauchy’ego pomiędzy średnimi

\[ H \le G \le A \]

czyli

\[ \frac{2 a_n\cdot b_n}{a_n + b_n} \le \sqrt{a_n \cdot b_n} \le \frac{a_n + b_n}{2} . \]

Mamy więc (\(n=1\)) - pamiętajmy, że średnia liczb zawsze ‘’leży pomiędzy nimi’’:

\[ a_0 < a_1 < b_1 < b_0 \]

i dalej

\[ a_0 < a_1 < a_2 < a_3 < a_4 < ... < b_4 < b_3 < b_2 < b_1 < b_0 . \]

Ciąg \((a_n)\) jest więc rosnący i ograniczony, a \((b_n)\) jest malejący i ograniczony. Oba są więc zbieżne, powiedzmy do \(a\) i \(b\), odpowiednio. Oczywiście \(a \leq b\). Pokażemy (dowód nie wprost!), że \(a = b\). Niech \(t = b-a\) i przypuśćmy, że \(t > 0\). Z definicji granicy: weźmy odpowiednio duże \(n\) tak, aby \(a - a_n < \frac{t}{2}\) oraz \(b_n - b < \frac{t}{2}\). Ale wtedy \(b_n - a_n > t\), czyli \(b_{n+1} < b\) - sprzeczność.

Przechodzimy do granicy w nierówności pomiędzy średnimi (i wykorzystamy, fakt że \(\sqrt{x_n} \to \sqrt{x}\) o ile tylko \(x_n \to x\) gdy \(n \to \infty\)).

\[ \frac{2 a\cdot b}{a+ b} \le \sqrt{a \cdot b} \le \frac{a + b}{2} . \]

Teraz wykorzystamy twierdzenie Cauchy’ego o średnich. W powyższej nierówności przy \(a = b\) zachodzi równość, czyli

\[ a_0 < a_1 < a_2 < a_3 < a_4 < ... \le \sqrt{1\cdot x} \le ... < b_4 < b_3 < b_2 < b_1 < b_0 . \]

\[ a = \sqrt{1\cdot x} = b . \]

Oba ciągi są zbieżne do \(\sqrt{x}\). To ważny algorytm oblicznia pierwiastka (liczby na og’{l} niewymiernej) na komputerze. Ale - będzie ich więcej…

Przykład 5. Wracamy do sytuacji z Przykładu (A). Mamy wtedy

\[ a_{n+1} = \frac{1}{2} \sqrt{2 - \sqrt{4- 4 a_n^2}} . \]

i wzór na obwód wielokąta to

\[ O_n = 2^n \cdot a_n . \]

Z samej konstrukcji (\(a_n\) to długość boku wielokąta) wiemy oczywiście, że \(0 < a_n < \sqrt{2}{2}\) (rozpoczynamy od kwadratu). Co więcej w każdym kroku dokonujemy podziału, czyli \(a_{n+1} < a_n\). A więc z samej konstrukcji wynika, że ciąg \((a_n)\) jest malejący.

A teraz pytanie otwarte: jak wykazać, że ciąg \((O_n)\) jest rosnący i ograniczony z góry?

Przykład 6. (samodzielnie) Dany jest ciąg:

\[ \sqrt{2} \ , \ \sqrt{2\sqrt{2}} \ , \ \sqrt{2\sqrt{2\sqrt{2}}} \ , ... \]

a) wyznaczyć wzór rekurencyjny,

b) sprawdzić zbieżność ciągu,

c) obliczyć granicę - o ile istnieje,

d) dodatkowe: znaleźć wzór ogólny!

Zadania domowe (?):

\[ a_0 = \sqrt{3} \ , \ a_{n+1} = \sqrt{3 + a_n} . \]

\[ b_0 = \sqrt{3} \ , \ b_{n+1} = (3 + b_n)^2 , \]

\[ f_0 = 0 \ , \ f_1 = 1 \ , \ f_{n+2} = f_{n+1} - f_n . \]

\[ y_0 = c = const. \ , \ y_{n+1} = \frac{1}{n+1} - 5\cdot y_n \]

(ostatnia relacja to obliczanie rekurencyjne pewnych całek - o czym później, tylko \(y_0\) należy obliczyć wstępnie).

Zadanie (Z1). Okres połowicznego rozpadu pierwiastka to okres, po którym z danej ilości pierwiastka pozostaje jego połowa. Dla radu (\(Ra\ 226\)) wynosi on 1560 lat. Ile lat co najmniej trzeba czekać, aby z \(1g\) radu zostało mniej niż \(0,1 mg\)?

Zadanie (Z2). Bezpośrednio za pomocą twierdzenia Cauchyego o średnich oraz twierdzenia o 3 ciągach wykaż, że \(\lim_{n \to \infty} \sqrt[n]{3} = 1.\) Czy tak samo można zbadać granicę \(\lim_{n \to \infty} \sqrt[n]{n} = 1\)?

Wstęp do matematyki 06-DPMALI0

13. Rekurencja 2.

13. Rekurencja 2.#